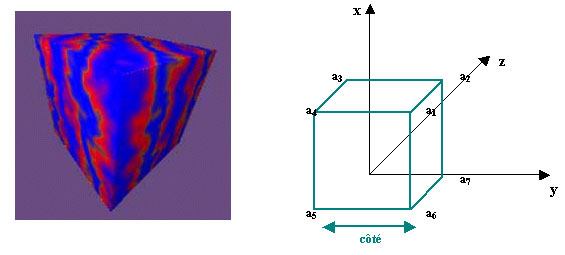
On définit les huit sommets et on utilise la méthode parallélogramme pour tracer le cube et relier correctement les sommets.

a1 = (côté/2 , côté/2 , -côté/2 , 1)
a2 = (côté/2 , côté/2 , côté/2 , 1)
a3 = (côté/2 , -côté/2 , côté/2 , 1)
a4 = (côté/2 , -côté/2 , -côté/2 , 1)
a5 = (-côté/2 , -côté/2 , -côté/2 , 1)
a6 = (-côté/2 , côté/2 , -côté/2 , 1)
a7 = (-côté/2 , côté/2 , côté/2 , 1)
a8 = (-côté/2 , -côté/2 , côté/2 , 1)

Puis on trace les faces avec la méthode parallélogramme pour (a1, a2, a4 ) , (a6, a7, a5 ) , (a1, a2, a6 ) , (a2, a7, a3 ), (a3, a8, a4 ) , (a4, a5, a1 )

Calcul de l'intersection

On calcule la distance entre le point d'intersection du rayon et de la face (a1, a2, a4 ) (méthode intersection de la classe parallélogramme). Si elle est différente de MAXDOUBLE, on affecte le numéro de la face intersectée à 0, sinon on l'affecte à -1. Puis, pour chaque face restante, on calcule une distance d' que l'on compare à d. Si d'<d, la face la plus proche intersectée est la face en cours, d'où le numéro de la face intersectée vaut le numéro de la face en cours, d prend la valeur de d', et le point d'intersection est mis à jour.

Calcul de la normale

Par défaut, on affecte les coordonnées de la normale à zéro.
Puis, selon la face considérée, on modifie ces valeurs de la manière suivante :

Selon la faceIntersectee
{
face (a1, a2, a4 ) :laNormalex = 1;
face (a6, a7, a5 ) :laNormalex = -1;
face (a1, a2, a6 ) :laNormaley = 1;
face (a2, a7, a3 ) :laNormalez = 1;
face (a3, a8, a4 ) :laNormaley = -1;
face (a4, a5, a1 ) :laNormalez = -1;
}