
Réalisation du lancer de
rayons
>> Lancer un rayon
>> Antialiasing
>> Atténuation
de la lumière
>> Ombres floues
>> Bruit de Perlin
>> Textures procédurales
>> Textures mapping
>> Bump mapping avec du bruit
de Perlin
>> Résolution
d'intersections pour les formes de bases
>> Résolution d'équations
algébriques de degrés 4
>> Ce qui reste à faire
...
DETAILS DES CALCULS POUR LE LANCER DE RAYONS
Le rendu par lancer de rayons est un processus récursif et additif, c'est à dire qu'à chaque intersection d'un rayon avec un objet, un ou plusieurs nouveaux rayons sont lancés dans des nouvelles directions fonctions des propriétés matérielles de la surface de l'objet, et que la valeur finale de la lumière au point d'intersection est la somme de la lumière directe en ce point, et de la lumière apportée par les rayons ré-émis.
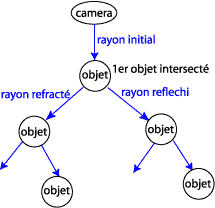
· Modélisation d'un rayon
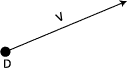
: Un rayon représente le trajet d'un photon, et donc n'a pas d'épaisseur.
Il est modélisé dans l'algorithme de lancer de rayons par
une demi-droite de l'espace, c'est à dire un point de départ
D et une vecteur directeur V. Ces deux paramètres sont suffisants
pour obtenir une équation paramétrée du rayon en
fonction du temps. Les points P(x,y,z) par lesquels passe le rayon sont
définis par P = D + tV, avec t>=0 . Une fois un rayon lancé,
il suffit de calculer son intersection avec les objets de la scène.
· Calcul d'intersections : Le calcul
de l'intersection d'un rayon avec les objets de la scène est la
base de la technique de lancer de rayons. En effet, pour chaque objet
composant la scène, il faut il faut obtenir les coordonnées
de son intersection (si elle existe) avec le rayon, et ne retenir que
l'objet le plus proche de la source du rayon. Ce calcul d'intersection
ne peut se faire que si l'on connaît l'équation implicite
de la surface représentant l'objet, de la forme S(x,y,z)=0. Pour
connaître le point d'intersection avec le rayon lancé, il
suffit de remplacer respectivement x, y et z de cette équation
par Dx+t.Vx , Dy+t.Vy et Dz+t.Vz , et de trouver la valeur t solution.
Une fois les coordonnées du point d'intersection connues, il est
facile de calculer la distance de ce point au point de départ du
rayon, et donc de déterminer l'objet le plus proche de la source
du rayon.
· Normale
au point d'intersection : Pour pouvoir connaître
les directions des nouveaux rayons à émettre depuis le point
d'intersection, il est indispensable de connaître la valeur de la
normale à la surface en ce point. Ce calcul est évident
pour les formes géométriques de base, mais peut nécessiter
des calculs plus poussés pour les objets plus complexes.

sans et avec anti-aliasing
La méthode de raytracing reposant sur l'utilisation de rayons de diamètre nul, il se crée sur les bords des objets un phénomène d'aliasing peu réaliste. Pour éviter cet effet de 'marches d'escalier', il existe plusieurs méthodes.
· Méthode naïve
: Au lieu de lancer un seul rayon par pixel, qui prendra pour intensité
la valeur de l'illumination du rayon passant par son centre, on lance
plusieurs rayons (4, 9, 16…) par pixel, uniformément répartis
sur la surface du pixel. La valeur finale de l'illumination est la moyenne
des valeurs de chaque rayon. Cette méthode donne de bons résultats,
mais multiplie les temps de calcul par le nombre de rayons que l'on décide
de lancer. La plupart des pixels n'ayant pas besoin d'être antialiasés,
cette méthode est trop lourde pour être acceptable.
· Méthode utilisée par notre
programme: Puisqu'il est inutile d'effectuer de l'antialiasing
pour tous les pixels, on ne lance qu'un seul rayon par pixel. Par contre,
la valeur de l'intensité trouvée pour ce pixel est comparée
à celle du pixel à gauche et du pixel au dessus. Si un écart
trop important est trouvé entre ces trois intensités (supérieur
au paramètre AA_THRESHOLD du fichier de description de scène),
on lance un nouveau rayon au hasard dans la surface du pixel, et l'on
moyenne avec la valeur précédente. Si la nouvelle valeur
du pixel est encore trop éloignée de la valeur des deux
voisins, on continue de lancer des rayons au hasard dans le pixel et de
moyenner avec la valeur précédente, jusqu'à arriver
soit à la profondeur maximale autorisée (paramètre
ANTIALIASING du fichier de description de scène), soit jusqu'à
obtenir une valeur conforme au paramètre du fichier de description
de scène. Cette méthode n'est pas infaillible, mais permet
dans une large majorité de cas d'obtenir un résultat acceptable,
et possède l'avantage de ne pas engendrer de calculs inutiles ralentissant
l'exécution du programme.
· Principe : L'atténuation
de la lumière peu être spécifiée à l'aide
de trois coefficients c1, c2 et c3 et ce uniquement pour les lumière
ponctuelles.
Un facteur d'atténuation fd est alors applique à chacune
de ces sources lumineuses, fd étant défini comme suit :
Fd = min( 1 / ( c1 + c2 * dist + c3 * dist*dist ) , 1 )
Dist étant la distance du point à illuminé à
la source lumineuse considérée.


sans et avec atténuation
· Dans notre raytracer
Voici comment spécifier l'atténuation pour une source lumineuse
dans notre raytracer :
Light_source {
Location <x,y,z>
Color <r,g,b>
Attenuation <c1,c2,c3>
}
· Principe : Le principal
problème dans une image rendue par lancer de rayon est que les
zones d'ombres propres et portées des objets sont très franches.
Il est cependant possible, mais pour un coût plus élevé
en calculs, de rendre celles-ci plus ou moins floues en utilisant une
petite astuce.
Celle-ci consiste à lancer pour chaque pixel de l'image, non un
seul, mais plusieurs rayons d'ombres vers chaque source lumineuse considérée,
en faisant bouger à chaque fois de façon aléatoire
ces mêmes sources lumineuses. Chaque rayon d'ombre lancé
va ou non apporter de la lumière sur le pixel en question, une
simple moyenne suffit alors à déterminer la luminosité
finale.
Les pixels situés à la limite d'une zone d'ombre vont donc
se trouver parfois illuminés et parfois dans l'ombre, et vont donc
constituer une limite en dégradé partant de l'ombre à
la lumière. Si les ombres floues sont activées , il est
alors préférable d'activer également l'antialiasing
afin de lisser encore plus les limites ombres -lumières.


sans et avec ombres floues
· Dans notre raytracer
Voici comment spécifier les ombres floues dans notre raytracer :
Global_setting {
Soft_Shadow x
Shadow_Ray y
}
y est un entier indiquant le nombre de rayons d'ombres à
générer pour chaque pixel
x est un nombre décimal indiquant l'intensité du déplacement
des sources lumineuses. Par exemple, si x vaut 2, cela signifie que les
sources lumineuses vont se déplacer dans un cube de taille 2, centré
sur leur position initiale.
Bien entendu, plus x est grand plus les ombres sont floues,
mais plus il faut augmenter y pour que les transitions soient uniformes.
Afin de modéliser des motifs complexes (nuages, marbres …), il est nécessaire d'avoir à disposition des algorithmes capables de les générer de façon automatique. Pour introduire une grande diversité et par ailleurs un meilleur réalisme, ces algorithmes se doivent d'introduire de l'aléatoire dans ces motifs. C'est l qu'intervient le bruit de Perlin, car bien entendu, il ne s'agit pas de générer des motifs totalement aléatoire, car on obtiendrait bien sur, dans ce cas, un motif " moucheté " du plus mauvais effet. Le bruit de Perlin, qualifié de bruit cohérent, permet de palier ce problème.
Bruit totalement aléatoire

Bruit de Perlin

De plus, il présente l'avantage de pouvoir s'écrire sous
le forme fNoise(x,y,z) et ainsi d'associer directement à un point
dans l'espace, une valeur qui peu ensuite être convertie en couleur
(pour faire de la texture procédurale) ou en hauteur (pour faire
du bumpmapping), ce qui est très pratique pour l'insérer
dans un moteur de raytracing. En effet la plupart des algorithmes de génération
de bruit cohérent (pour générer des montagnes fractales
par exemples), créent les motifs de proche en proches de façon
récursive et ne peuvent donc associer de façon directe une
valeur à un point.
Le principe pour générer du bruit de Perlin est d'additionner plusieurs fonctions de bruit d'amplitude et de fréquence différentes, ce qui permet d'avoir cet effet de cohérence dans le bruit généré. Voici un exemple ci-dessous :
Bruit de Perlin avec fonction à une dimension :
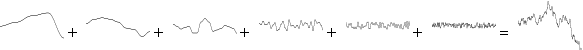
Bruit de Perlin avec fonction à deux
dimensions :
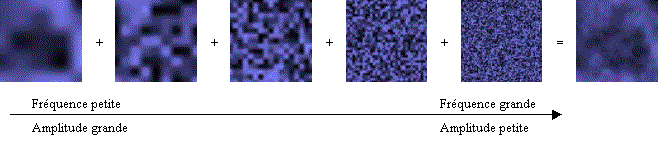
Il s'agit ici de déterminer la couleur de tout point
de coordonnées (x1, x2, x3) dans le repère de la scène
à l'aide d'une procédure.
On peut ainsi définir toute sorte de procédures. En voici
2 exemples :
· Checker
Le checker est défini par 2 couleurs c1, c2 et la longueur L des
carreaux.
Ici on calcule la parité pi de la partie entière de xi /
L.
Si xi < 0 alors on prends la parité inverse.

Voici l'algorithme déterminant la couleur en fonction des pi :

· Perlin
La couleur d'un point peut être donnée à partir d'un
bruit de Perlin. Ceci nous permet d'obtenir des textures très réalistes
comme le bois ou le marbre.
· Bruit de perlin seul
Pour appliquer le bruit de perlin comme texture procédurale,
il suffit de demander pour chaque point (x,y,z) dont on veut connaître
la couleur, la valeur n de fNoise(x,y,z). Selon la valeur de n, on interpole
alors une couleur à partir d'une table de couleur.

Par exemple :
Soit la table de couleur suivant :
Si n = v1 alors couleur = (r1,g1,b1)
Si n = v2 alors couleur = (r2,g2,b2)
Si n = v3 alors couleur = (r3,g3,b3)
Si n = v4 alors couleur = (r4,g4,b4)
Avec v1 < v2 < v3 < v4
Si v2 < n < v3, alors on prendra comme la couleur (r,g,b)
avec :
r = r2 * (n-v2) / (v3-v2) + r3 * (v3-n) / (v3-v2)
g = g2 * (n-v2) / (v3-v2) + g3 * (v3-n) / (v3-v2)
b = b2 * (n-v2) / (v3-v2) + b3 * (v3-n) / (v3-v2)
· Effet marbré
Pour obtenir un effet marbre, il suffit de remplacer fNoise(x,y,z) par
:
fMarbre(x,y,z) = cos( x + fNoise(x,y,z) )
· Effet bois
Pour obtenir un effet bois, il suffit de remplacer fNoise(x,y,z) par :
v = 20 * fNoise(x,y,z)
fBois(x,y,z) = v - partieEntiere(v)

· Dans notre raytracer
Voici comment spécifier ces textures procédurales dans notre ray-tracer :
Objet {
PARAMETRES_OBJET
Pigment {
Perlin {
amplitude,frequence,octave,intensite
}
Scale <sx,sy,sz>
Rotate <rx,ry,rz>
Translate <tx,ty,tz>
}
}
intensite est un coefficient multiplicateur appliqué
au bruit
octave est le nombres de fonctions de bruit additionnée
frequence est la fréquence de la fonction de bruit
amplitude est l'amplitude de la fonction de bruit
rotate, translate et scale sont des transformation apportées sur le motif de la texture procédurale.
Pour l'effet marbre il suffit de remplacer le mot clé perlin par marble et pour l'effet bois de remplacer perlin par wood.
Le principe est d'appliquer une image sur une surface, de
façon répétitive ou non.
Il faut donc faire correspondre un point de l'image à chaque point
de la surface considérée.
Pour permettre cette correspondance il nous faut tout d'abord
déterminer un paramétrage de la surface :
x = fx(u, v)
y = fy(u, v)
z = fz(u, v)
Puis nous faisons correspondre à (u, v) un pixel (i, j) de l'image.
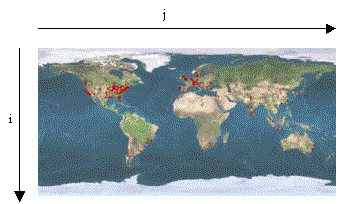
· Mapping sur le cercle
Les équations paramétriques du cercle sont les suivantes :
x = r sin u
y = r cos u sin v
z = r cosu cos v
u varie dans [-pi /2, pi/2] et v varie dans [0, 2pi[.
Soit n la fréquence de répétition de l'image sur la sphère, H la hauteur de l'image, L sa largeur.
Calcul du pixel i correspondant au paramètre u :
t = n ( u / P + 0.5)
i = PartieEntière ( H (t-PartieEntière(t))
Calcul du pixel j correspondant au paramètre v :
t = n ( u / (2P))
j = PartieEntière ( L (t-PartieEntière(t))
Pour n = 1 on obtient le résultat suivant :
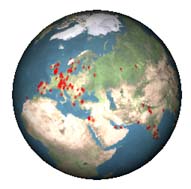
· Mapping sur le plan
Les équations paramétriques du plan d'équation
x = 0 sont les suivantes :
x = 0
y = v + n/2
z = u - m/2
Soit n la largeur désirée de l'image sur le plan, H la hauteur
de l'image, L sa largeur initiale et m la hauteur sur le plan égale
à n.H / L.
Calcul du pixel i correspondant au paramètre u :
t = m.PartieEntière(u / m)
i = PartieEntière ( H (u - t) / m)
si i < 0 alors i = -i.
Calcul du pixel j correspondant au paramètre v :
t = n.PartieEntière(v / n)
j = PartieEntière ( L (v - t) / n)
si j < 0 alors j = -j.
Ainsi, dans le cas suivant :
- camera "orthographique" définie avec une largeur de
projection de n,
- un plan parallèle à la camera à qui on applique
l'image avec une largeur de n,
- une image de sortie de la même taille (H.L pixels) que l'image
appliquée sur le plan,
on obtient une image de sortie identique à l'image appliquée,
hormis les effets de lumières, d'ombres, de réflexions ou
de transparences apportés par le lancé de rayon.
BUMP MAPPING avec du bruit de Perlin
· Principe
Le bump-mapping est une technique permettant de donner un aspect non lisse
à un objet géométriquement lisse. Il consiste en
l'altération des normales d'un objet, ce qui modifie par la même
l'illumination des points de l'objet situés à la base de
la normale.

La technique utilisée ici est d'utiliser le même bruit de perlin que pour les textures procédurales, mais de considérer les valeurs fournis par la fonction de bruit, non pas comme une couleur, mais comme une hauteur.
· Dans notre raytracer
Voici comment spécifier du bump-mapping dans notre
raytracer :
Objet {
PARAMETRES_OBJET
Pigment { … }
Normal {
Perlin {
amplitude,frequence,octave,intensite
Scale <sx,sy,sz>
Rotate <rx,ry,rz>
Translate <tx,ty,tz>
}
}
}
Pour modifier la normale au point (x,y,z) d'une surface, on crée le vecteur v dont les directions x,y et z suivent les variations du bruit de perlin autour d'un point considéré :
V[0] = fNoise (x-e,y,z) - fNoise (x+e,y,z)
V[1] = fNoise (x,y-e,z) - fNoise (x,y+e,z)
V[2] = fNoise (x,y,z-e) - fNoise (x,y,z+e)
On altère ensuite la normale au point (x,y,z)
en lui additionnant v. Reste seulement a choisir les bon paramètres
pour générer le bon bruit de perlin !
RESOLUTION D'INTERSECTIONS
POUR LES FORMES DE BASES
L'algorithme de raytracing engendre un nombre très
important de calculs sur des nombres réels, dont la majeure partie
consiste à déterminer des intersections objet-rayon. La
résolution des problèmes d'intersections revient essentiellement
à trouver les racines de polynômes, jusqu'au 4eme degré
pour le tore et le cube troué.
Les calculs d'intersections et de
normales
Chaque objet de la scène est défini dans son repère
propre. Lors de la description de la scène, les paramètres
de translation, rotation et mise à l'échelle permettent
de définir une matrice de transformation propre à chaque
objet, qui permet de passer des coordonnées de points ou de vecteurs
dans le repère absolu à celles dans le repère de
l'objet, et inversement. Cette transformation se fait grâce à
des produits matrice-vecteur, et n'est possible que parce que l'on utilise
des coordonnées homogènes pour représenter les points
de l'espace.
Pour chaque objet, il suffit de définir les méthodes calculant
l'intersection avec un rayon et la normale en un point ; il est donc aisé
d'ajouter de nouveau objets au programme.
Dans la fonction intersection, on calcule le point d'intersection entre
le rayon et l'objet. Pour cela, il est tout d'abord nécessaire
d'appliquer la matrice inverse de transformation sur le rayon pour que
ce dernier soit dans le même repère que l'objet. Par la suite,
il faut effectuer le calcul d'intersection propre à chaque objet,
que l'on détaille en annexe. Pour finir, on applique la matrice
de transformation sur le point d'intersection pour le ramener dans le
repère de la scène, et on retourne la valeur de la distance
entre ce point d'intersection et le point origine du rayon.
Pour le calcul de la normale au point d'intersection, il est également
nécessaire d'utiliser la matrice inverse de transformation pour
placer le point d'intersection dans le repère de l'objet. Le rayon
est transformé dans le repère de l'objet. Puis on prend
en compte le côté d'où provient le rayon par rapport
à l'objet (intérieur, extérieur, dessus, dessous)
à l'aide du produit scalaire du rayon et de la normale. Pour finir,
on normalise cette normale, et on lui applique la matrice de transformation
pour la replacer dans le repère de la scène.
Les équations mathématiques à résoudre pour
chaque objet sont détaillées ci-dessous.
>>
cone
>> cube
>> cubeTroue
>> cylindre
>> parallélogrammme
>> plan
>> prisme
>> pyramide
>> sphere
>> tore
>> triangle
RESOLUTION D'EQUATIONS
POLYNOMIALES DE DEGRES 4
Pour trouver les racines de polynômes jusqu'au
degré 4, nous utilisons la méthode de François Vieta,
qui date de 1735.
Soit à résoudre
![]()
Le cas où a3 et a4 sont nuls, ce qui revient à
résoudre une équation du 2nd degrés, n'est pas traité
ici. En effet ce cas est considéré comme trivial.
Ici la résolution proposée est purement algébrique.
Cas où a4 est nul et a3 non nul : résolution d'une équation du 3ième degrés

Cas où a4 est non nul : résolution
d'une équation du 4ième degrés
Methode de Francois Vieta (1735)


CE QUI RESTE A FAIRE...
Notre programme permet d'obtenir des images photoréalistes
de qualité, meilleures que l'algorithme du z-buffer combiné avec ceux
de Gouraud ou Phong qui ne prennent pas en compte la réflexion et la réfraction.
D'autre part, le lancer de rayon ne se limite pas comme les algorithmes
précédents à la seule visualisation des modèles facétisés, c'est à dire
composé exclusivement de polygones. Il permet la visualisation de surfaces
implicites. Cependant, les temps de calculs sont généralement considérablement
longs et la visualisation ne peut pas se faire en temps réel comme avec
le z-buffer. De plus il est de moins bonne qualité que l'algorithme de
radiosité qui modélise mieux les phénomènes de transport d'énergie.
L'une des améliorations à apporter à notre programme est d'implémenter le lancer de rayons arrière. Cette méthode consiste à lancer des rayons depuis les sources de lumière vers la scène, permettant de déterminer les sources de lumière secondaires (la réflexion de la source de lumière sur un miroir par exemple), afin d'obtenir des résultats plus réalistes.
Notre " raytracer " traite
des scènes comportant des objets de base relativement simples, mais néanmoins
suffisants pour construire des scènes intéressantes. Il serait possible
de rajouter quelques objets de bases supplémentaires, tels que :
·
les ellipsoïdale, hyperboloïdale
(formes super-quadratiques) d 'équations implicites de la forme : (x/a)2/p
+ (y/b)2/p + (z/c)2/q = 1 ou (x/a)2/p + (y/b)2/p - (z/c)2/q = 1
· les meta-balls d 'équations implicites
de la forme : a1 * exp ( - b1 * f1 (x,y,z)) + ... + an * exp ( - bn *
fn (x,y,z)) = 0.
· des objets plus complexes tels que les Constructive
Solid Geometry (C.S.G.), arbres dont les feuilles sont des volumes
simples.
Le calcul d'intersections constituant la majeure quantité de calculs à effectuer, il y aurait plusieurs façons pour pouvoir accélérer cette partie. En effet, nous avons ici traité la méthode naïve consistant à calculer l'intersection d'un rayon avec toutes les surfaces de la scène puis à sélectionner la plus proche. La première optimisation est de diminuer le nombre de rayons primaires en projetant les objets de la scène sur l'écran. La deuxième est l'utilisation des volumes simples englobants un ensemble d'objets, à savoir que si un rayon n'intersecte pas ce volume, il est inutile de faire le calcul d'intersection avec tous les objets qu'il contient. Mais la génération de ces volumes englobants s'est avérée problématique. Une autre solution est de décomposer l'espace en voxels, puis à l'aide de méthodes incrémentales (de type Bresenham) on détermine la succession de voxels rencontrés par le rayon et donc les objets susceptibles d'intersecter le rayon, ce qui réduit les temps de calcul. Pour obtenir une bonne efficacité, il faut un grand nombre de voxels et le coût mémoire sera donc énorme. La technique de l'arbre octal tente de palier à cet inconvénient : la scène est divisée en 8 voxels jointifs, et eux-même divisés en sous voxels, récursivement tant qu'un voxel contient un nombre trop important d'objets. Cette méthode permet de créer un arbre non-symétrique où 8 branches partent de chaque nœud, et où chaque feuille est une liste d'objets contenus dans le voxel correspondant. L'arbre octal réduit considérablement le coût mémoire de par la moindre occupation des zones vides.