Le tore est défini dans son propre repère à l'aide de ses deux rayons r et R.

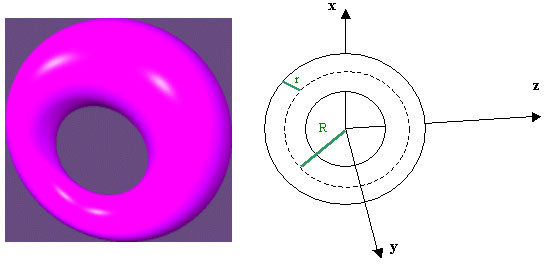
Calcul de l'intersection

L'équation du rayon est :
x(t)= d0 t+p0
y(t)= d1 t+p1
z(t)= d2 t+p2
avec (d0,d1,d2)la direction du rayon et (p0 ,p1 ,p2 ) le point origine du rayon.

L'équation du tore est (x² + y² + z² + R² - r²)² - 4 R² (x² + z²) = 0.
On résout donc ((d0 t+p0)² + (d1 t+p1)² + (d2 t+p2)² + R² - r²)² = 4R²( (d0 t+p0)²+ (d2 t+p2)²).
Ce qui nous donne une équation du quatrième ordre a t4 + b t3 + c t² + d t + e = 0, avec
a = (d0² + d1² + d2²)²
b = 4 (d0² + d1² + d2²)(d0 p0 + d1 p1 + d2 p2)
c = 2 (d0² + d1² + d2²)(p0² + p1² + p2² + R² - r²) + (d0 p0 + d1 p1 + d2 p2)² - 4 R² (d0² + d2²)
d = 4 (d0 p0 + d1 p1 + d2 p2) (p0² + p1² + p2² + R² - r²) - 8 R² (d0 p0 + d2 p2)
e = (p0² + p1² + p2² + R² - r²)² - 4 R² (p0² + p2²)
On résout cette équation avec la méthode utilisée dans la classe polynomiale (méthode de Vieta).
S'il existe des racines réelles, on choisit la racine t0 minimum supérieure strictement à epsilon.
Si celle-ci existe, on calcule le point d'intersection entre le tore et le rayon avec t= t0 dans l'équation paramétrique du rayon.
Dans le cas ou toutes les racines sont inférieures à epsilon, t a pour valeur MAXDOUBLE et donc le rayon ne rencontre pas le tore.

Comme pour les autres objets, la distance est évaluée lorsqu'il existe un point d'intersection. Sinon, elle vaut MAXDOUBLE.

Calcul de la normale

Ici pour le calcul de la normale nous allons utiliser le gradient de l'équation implicite f(x, y, z) = 0 définissant la surface du tore.
f(x,y,z) = (x² + y² + z² + R² - r²)² - 4 R² (x² + z²)

df/dx = 4 x (x² + y² + z² + R² - r²) - 8 R² x
df/dy = 4 y (x² + y² + z² + R² - r²)
df/dz = 4 z (x² + y² + z² + R² - r²) - 8 R² z

Ainsi au point (x, y, z) la normale a pour coordonnée (df/dx, df/dy, df/dz).