Le prisme est défini par quatre points : a1, a2, a3, a4. On trace les faces avec la méthode triangle pour (a1, a2, a3 ) , (a1, a2, a4 ) , (a1, a3, a4 ), (a3, a2, a4 ).

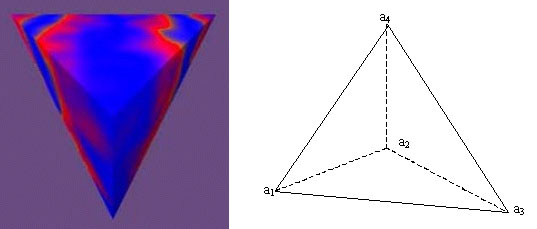
Calcul de l'intersection

On calcule la distance entre le point d'intersection du rayon et la face (a1, a2, a3), à l'aide de la méthode intersection de la classe triangle. Si elle est inférieure à MAXDOUBLE, on affecte le numéro la variable face intersectée à 0, sinon on lui affecte la valeur -1. Puis, pour chaque face restante (de 1 à 3), on calcule une distance d' (méthode intersection de la classe triangle) que l'on compare à d. Si d'<d, la face la plus proche intersectée est la face en cours, d'où le numéro de la face intersectée vaut le numéro de la face en cours, d prend la valeur de d', et le point d'intersection est mis à jour.

Calcul de la normale

Si le numéro de la face intersectée est différent de -1, on utilise la méthode normale de la classe triangle pour calculer la normale.