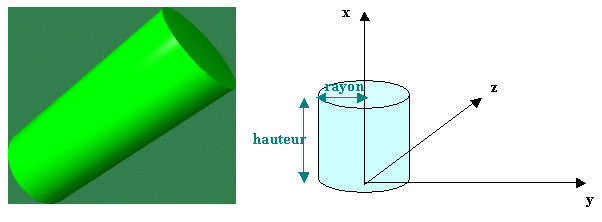
Il existe deux constructeurs différents pour le cylindre. Le cylindre peut être défini uniquement par son rayon si l'on souhaite avoir un cylindre infini. Dans ce cas, on affecte la longueur par défaut à la valeur nulle.
Le cylindre peut également être défini d'après son rayon et sa hauteur si l'on veut un cylindre fini. Dans tous les cas, le cylindre est orienté selon l'axe des x.

Calcul de l'intersection

Il faut calculer le point d'intersection entre le rayon et le cylindre.

L'équation du rayon est :

Pour le cylindre, on a pour x compris entre 0 et hauteur :

Donc :

D'où :

On résout donc un équation du second ordre. Soit Delta son discriminant.

Si Delta est négatif, cela signifie qu'il n'y a pas de solutions à l'équation. On affecte donc la distance par défaut à la valeur MAXDOUBLE. Plusieurs possibilités sont alors envisageables.

Si , cela signifie que l'on se situe dans l'alignement du cylindre.
Si le cylindre est fini et que p0 est supérieur à la hauteur du cylindre ou que p0 est positif et inférieur à la hauteur, cela signifie que le rayon rencontre la face supérieure du cylindre.

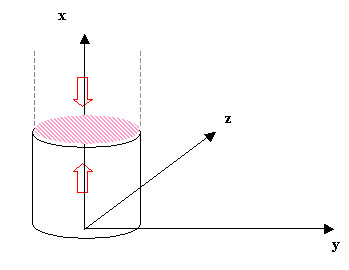
Ce calcul d'intersection peut alors être ramené au calcul d'intersection d'un rayon et d'un plan en x = hauteur :
x(t)= d0t+p0 = hauteur donc t = ( hauteur - p0 ) / d0 si d0 est non nul.
Puis on remplace t dans les équations y(t), et z(t) du rayon pour obtenir les coordonnées du point d'intersection.

Si le cylindre est fini et que p0 est négatif ou que p0 est positif et inférieur à la hauteur, cela signifie que le rayon rencontre la face inférieure du cylindre.

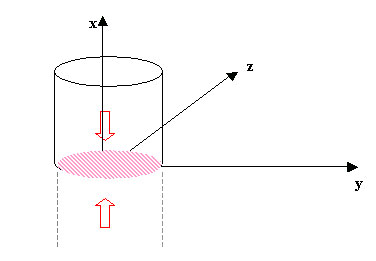
On résout donc :
x(t)= d0t+p0 = 0 donc t = - p0 / d0 si d0 non nul.
Puis on remplace t dans les équations y(t), et z(t) du rayon pour obtenir les coordonnées du point d'intersection.

Si Delta est positif, on calcule les deux racines de l'équation t1 et t2.

Si le cylindre est fini et si t1 est inférieur à t2 et supérieur à epsilon, ou si t2 est inférieur à t1 et inférieur à epsilon, la racine correcte est t1, sinon c'est t2.
On calcule alors les coordonnées du point d'intersection en remplaçant t par sa valeur dans les équations x(t), y(t) et z(t) du rayon et on calcule la distance séparant ce point du point p du rayon.
Il faut néanmoins considérer deux autres cas. En effet, on peut se trouver dans les situations suivantes :

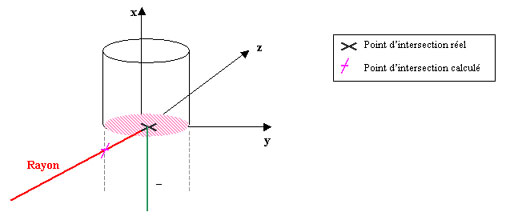
Donc plusieurs cas se présentent :
· Si le cylindre est fini et que l'abscisse du point d'intersection calculé est inférieur à zéro (en rouge ci-dessus), ou que l'abscisse du point initial est inférieur à zéro, et que (en vert ci-dessus), on se situe sur la face inférieure du cylindre, donc comme précédemment, on résous :
x(t)= d0t+p0 = 0 donc t = - p0 / d0 si d0 non nul, sinon on renvoie MAXDOUBLE. Puis on remplace t dans les équations y(t), et z(t) du rayon pour obtenir les coordonnées du point d'intersection.
Si t est supérieur à epsilon et que le point d'intersection est tel que , on calcule la distance entre le point d'intersection et le point origine du rayon, sinon on renvoie MAXDOUBLE.
· Si le cylindre est fini et que l'abscisse du point d'intersection calculé est supérieur à la hauteur du cylindre, ou que l'abscisse du point initial est supérieur à la hauteur du cylindre, et que p12 + p22 £ rayon2 :
x(t)= d0t+p0 = hauteur donc t = ( hauteur - p0 ) / d0 si d0 ¹ 0, sinon on renvoie MAXDOUBLE. Puis on remplace t dans les équations y(t), et z(t) du rayon pour obtenir les coordonnées du point d'intersection.
De même que précédemment, si t est supérieur à epsilon et que le point d'intersection est tel que , on calcule la distance entre le point d'intersection et le point origine du rayon, sinon on renvoie MAXDOUBLE.

Tous les cas sont alors correctement traités.

Calcul de la normale

La coordonnée homogène est égale à 0.
Si l'on se situe sur le côté du cylindre, c'est-à-dire si le cylindre est infini, ou si le cylindre est fini et que le point d'intersection est situé à une abscisse comprise entre 0 et hauteur, la normale est égale à 0 pour la composante en x, et le point lui-même divisé par la coordonnée homogène pour les composantes en y et z.
Si l'on se situe sur la face inférieure du cylindre, la composante en x vaut -1, les autres 0.
Enfin, si l'on se situe sur la face supérieure du cylindre, la composante en x vaut 1, les autres 0.