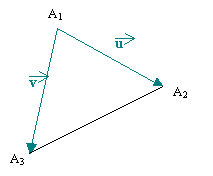
Le triangle est défini dans le repère de la scène par trois points A1, A2, A3.
On représente le triangle de la manière suivante :

Calcul de l'intersection

Il faut calculer le point d'intersection entre le rayon et le triangle, qui doit être illuminé.

L'équation du rayon est :

Pour obtenir la normale au triangle, il faut réaliser le produit vectoriel entre les vecteurs u et v. Puis on va chercher l'intersection entre le rayon et le plan défini par le triangle. Cette intersection existe seulement si le plan et le rayon ne sont pas parallèles, donc si le produit scalaire entre la normale au plan et le rayon est non nul, c'est à dire (u ^ v).d n'est pas nul.
Le point d'intersection I(x, y, z) entre le plan (A, u, v) et le rayon vérifie le système d'équations suivantes :

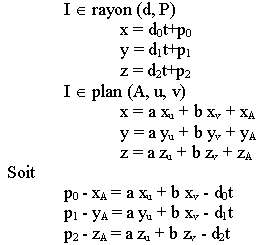
les inconnus de ce système sont t, a et b et le déterminant est D = -(u ^ v).d

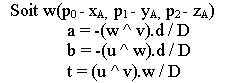
Le point d'intersection I est dans le triangle si et seulement si :
a et b sont positifs
a + b inférieur ou égal à 1

Comme pour les autres objets, la distance est évaluée lorsqu'il existe un point d'intersection. Sinon, elle vaut MAXDOUBLE.

Calcul de la normale

Pour le calcul de la normale au triangle, on effectue le produit vectoriel entre les vecteurs u et v.