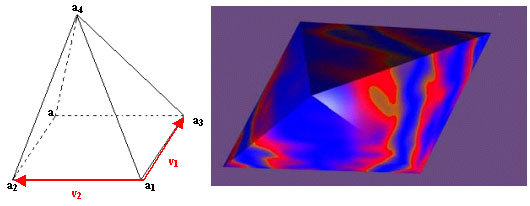
La pyramide est définie par quatre points : a1, a2, a3, a4. Le point a ainsi que les vecteurs v1 et v2 sont calculés par le programme.

v1 = (p2x-p1x,p2y-p1y,p2z-p1z};
v2 = (p3x-p1x],p3y-p1y,p3z-p1z};
a = (p1x+v1x+v2x,p1y+v1y+v2y,p1z+v1z+v2z,1};

On utilise les méthodes parallélogramme et triangle pour tracer la pyramide et relier correctement les sommets.
On trace la base avec la méthode parallélogramme pour (a1, a2, a3 ). Puis on trace les autres faces avec la méthode triangle pour (a1, a2, a4 ) , (a2, a, a4 ) , (a, a3, a4 ), (a3, a1, a4 ).

Calcul de l'intersection

On calcule la distance entre le point d'intersection du rayon et de la base (a1, a2, a3, a), à l'aide de la méthode intersection de la classe parallélogramme. Si elle est inférieure à MAXDOUBLE, on affecte le numéro 100 à la variable face intersectée, sinon on lui affecte la valeur -1. Puis, pour chaque face restante (de 0 à 3), on calcule une distance d' (méthode intersection de la classe triangle) que l'on compare à d. Si d'<d, la face la plus proche intersectée est la face en cours, d'où le numéro de la face intersectée vaut le numéro de la face en cours, d prend la valeur de d', et le point d'intersection est mis à jour.

Calcul de la normale

Si le numéro de la face intersectée est différent de -1, plusieurs cas se présentent :
· Si la face intersectée est la base, on utilise la méthode normale de la classe parallélogramme
· Si c'est une autre face, on utilise la méthode normale de la classe triangle